目录 / Table of Contents
本文以单精度浮点格式(即C++中的float类型)为例,简要介绍 IEEE754 标准中浮点数的表示方法,以及该表示方法中需要特别注意的部分(即浮点数中的阶码是以移码形式存储的),并基于上述两点,求得单精度浮点数的有效数字的位数以及取值范围。其他类型浮点格式的有效数字位数及取值范围可依此类推。
前置知识
若想了解浮点数在计算机内被如何存储,就必须先了解 IEEE754 标准,which 制定了计算机内浮点数及其运算的标准,被目前几乎所有的计算机所支持。
IEEE754 标准
根据IEEE浮点数标准,一个浮点数可表达为: $$ V=(-1)^s \times M \times 2^E $$
其中,
- V 表示所表示的浮点数的实际值
- s 为符号位(Sign),表示该浮点数为正数或负数。若为正数,则 s 取值为0;若为负数,则 s 取值为1 (注:对于数值0的符号位需要特殊处理)
- M 为尾数(Mantissa),是一个二进制小数,用于确定浮点数的精度,以定点数的形式存储在计算机内部(注意:此处的尾数的形式实为1.ffffff,而非0.fffffff,这个特征在下文讨论移码时会被重新提及)
- E 为阶码(Exponent),用于对浮点数进行加权 (!!!注意!!!:阶码的取值可正可负,是一个有符号数,分别代表小数点是向左移还是向右移。出于使用上的便利,在存储阶码时用到了特别的方式,即下文即将提到的移码(Excess-N System) )
将浮点数的位表示划分为三个字段,并分别对这些值进行编码,便可表示出浮点数的实际值。以单精度浮点格式为例。在单精度浮点格式中,符号位s、阶码E和尾数M的尾数分别为1位、8位和23位,将三者联立便可得到以32位表示出的浮点数,具体形式可参见下图:
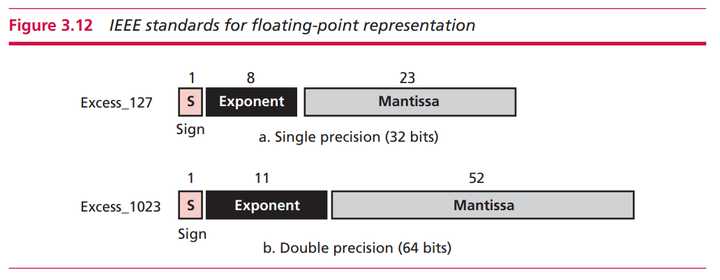
图源:Foundations of Computer Science (2018), Behrouz Forouzan
阶码的存储形式——移码 (Excess-N System)
为啥不能用补码存储阶码?
在上文中我们提到,阶码 E 是一个有符号数,用于表示小数点需要向左或向右移动的位数。那么,在存储阶码时,根据此前所学的知识,我们自然会想到以补码 (2’s complement) 的形式存储阶码。
但是,我们在课本上看到的阶码可不是用补码表示的。这是为什么呢?说实话,我不太确定真正的原因,现在能想到的理由如下:以补码表示的阶码会出现一个新的符号位(区别于上文 IEEE754 标准中所提到的符号位s),使得一个浮点数中出现两个符号位:浮点数本身的,以及浮点数阶码前的。这时,如果要对浮点数进行运算或者比较,无法采用整数那样的简单的二进制比较,所以算起来并不方便。
那有啥更好的方法存储阶码?
既然不能用补码,那我们只能另辟蹊径了。回顾用补码表示阶码所产生的问题,可以发现,阶码作为有符号数时具备的符号位是引发麻烦的源头,那么为了方便起见,只能想着除去符号位了。基于这种思想,前人提出了移码(Excess-N System)的存储方式。简单而言,补码在存储阶码时所起到的作用,便是对于 作为有符号数的阶码 的所有可能取值,分别增加一个特定的值N(即$2^{m_E-1}-1$,也是上文中Excess-N中N的含义),从而将原本所有可能的取值映射到一个新的正数集合。基于该正数集合,我们可以找出与原阶码一一对应的无符号数。通过移码,我们不再需要考虑如何处理原本作为有符号数的阶码所包含的符号位(因为阶码的所有可能取值已经被我们映射到了一个正整数集合)。因此,当我们需要对阶码进行运算或比较时,便可以将这些运算或比较先作用于新的整数集合上,再通过映射的逆操作得到我们所需的阶码值。
等等……上面那个用于增加的值 $2^{m_E-1}-1$ 是啥玩意儿?
至此,移码在阶码存储中的用途便讲得差不多了……不过,我是不是忘了什么?哦,在读上面那段的时候,你可能在想,那个$2^{m_E-1}-1$是啥?简单来说,这是将有符号数的阶码全部映射成正整数的一个比较合适的取值,其中$m_E$ 表示的是存储阶码可用的存储单元的位数,在单精度浮点格式里是8位。
还是以单精度浮点格式为例。上文中,我们提到,作为有符号数的阶码有正有负,在单精度浮点格式里的取值范围是 -126~127 (为啥不是 -128~127 ? 在定义移码的时候,我们是以定点小数0.ffffff作为尾数 M 的,这样算出来的阶码范围确实是-128~127。但是,尾数 M 实际上并不是这么被定义的—— IEEE754 中,尾数 M 是被规范化为1.ffffff,而非0.ffffff,因此要将尾数 M 的小数点左移一位,才符合移码的定义,也就是在此前算出来的阶码范围的基础上加1,即-127~128。在此基础上,还需要掐头去尾,从而得到-126~127)。与此同时,8位无符号数的取值范围为0~255,但是因为 $(0000 0000)_2$ 和 $(1111 1111)_2$ 有着特殊含义,所以需要去除这两个数,使得无符号数的取值范围变为1~254。那么,对于-126~127,只需增加127,就能完成从-126~127到1~254的映射。
总而言之,我们在存储阶码时,实际上是以无符号数的形式完成存储的。只不过,这些无符号数的取值并非阶码的实际值,而是由(本应是有符号数的)阶码的实际值统一增加$2^{m_E-1}-1$个单位得到的。
float类型浮点数的取值范围
默认存储的数值为规格化数的前提下进行的。而在IEEE 754标准中规定,当指数位阶码均为1时,该数取值为 NaN 或 $\pm \infty$ ;当指数位阶码均为0时,则表示0。这两种情况均不属于规格化数,因此可知,当数位和尾数位取得可能取值的最大值,即: