今天读 Mathematical Foundations for Finance 讲义里的布朗运动一章时,看到布朗运动的轨道满足一个以前没见过的 Law of the iterated logarithm,内容如下:
假设 $W=(W_t)_{t \geq 0}$ 是一个布朗运动,那么我们有:
$$ \begin{align} & \limsup\limits_{t \rightarrow \infty} = \frac{W_t}{\psi_{\text {glob }}(t)}=1, \mathbb{P}\text{-a.s.,} \\ & \liminf\limits_{t \rightarrow \infty} = \frac{W_t}{\psi_{\text {glob }}(t)}=-1, \mathbb{P}\text{-a.s.,} \end{align} $$
其中 $\psi_{\text {glob }}(t) := \sqrt{2t \log (\log t)}$。
粗糙点讲,这里 Law of the iterated logarithm 的含义是, 布朗运动的的样本路径几乎是被包含在 $\pm \psi_{\text {glob }}(t) $ 所组成的上下界内的。不过,由于这里是 $\lim \sup$,而非 $\sup$ ,所以样本路径有时候也会越过上下界。
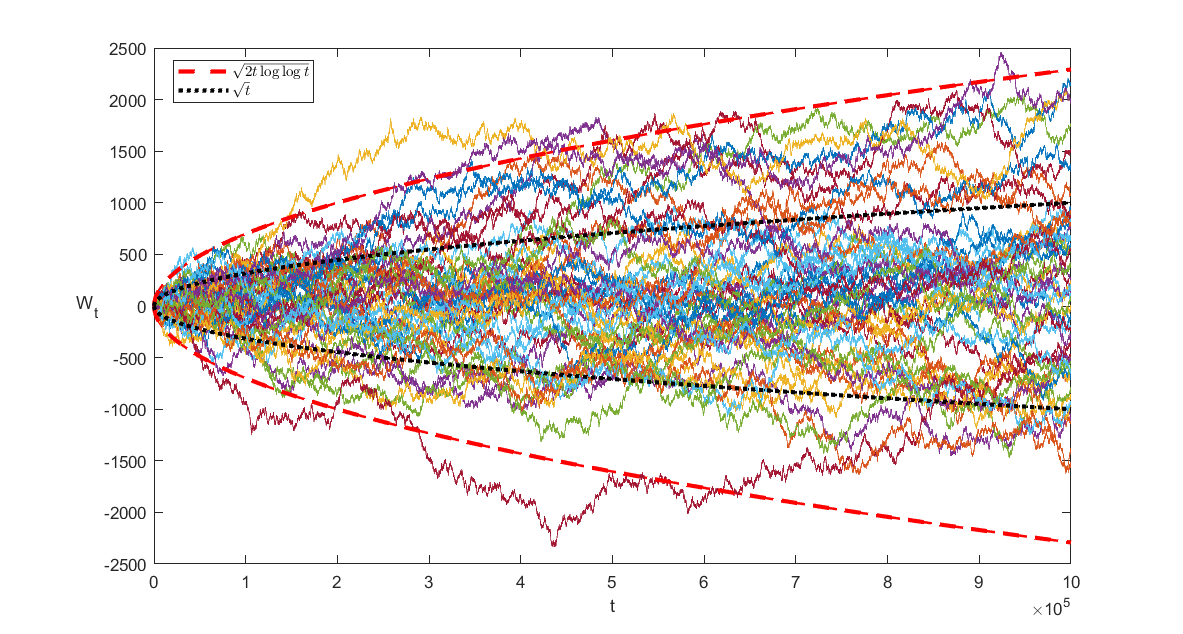
t=1E6 且 n_path=500 时的布朗运动
另外,重对数律也可被理解为大数定律与中心极限定理的「边界」,相关阐述可见于:为什么我觉得大数定理和中心极限定理是矛盾的? - 知乎 (zhihu.com)。