目录 / Table of Contents
Cyberbullying
The following passage are an excerpt from a TED speech about cyberbullying (and I’ve forgotten the full name of this speech).
When chatting online, we may think our words are just the words. We don’t need to take responsibility for what we have said, even when our words really hurt others – we just keep silent, having no courage to confess it.
Social network is basically a mutual approval machine. We just surround ourselves with people who feel the same way we do, and we approve each other. That’s a really good feeling.
The greatest thing about social media is how it gives a voice to voiceless people. I still remember the early days of social network, when people admit shameful secrets about themselves, and others would say, “Oh, that’s also what I’m thinking about.”
But now, we are creating a surveillance society, where every one of us may fall the victim to the cyberbullying. You may lead a good, ethical life, but some bad phraseology on social network can overwhelm it all, becoming a clue to your so-called “secret inner evil”.
Under this circumstance, maybe the smartest way to survive is to go back to being voiceless. However, if we just hang back and reserve, doing nothing, we will find that the situation get even worse. People may just create a stage for artificial high dramas, where everybody is either a magnificent hero or a sickening villain, even though we know that’s not true about our fellow humans. What is really true, is that we are clever and stupid, that we are all living in grey areas.
MISC
Schaut her, schaut her, schaut keinem ins gesicht.
Hallo!
Hallo. Wie heißen Sie?
Ich heiße GDR. Woher kommen Sie?
Ich komme aus China.
So, wo wohnen Sie?
Ich wohne in Shanghai.
O, ich wohne auch in Shanghai.
Wohin kommst du?
Ich komme nach Deutschland.
如何方便计算事件的概率——随机变量与分布
给事件贴上实数类型的标签——随机变量 $X$
我们已经有了一系列的公理概念。但是，我们考察的对象都是集合这一类型。如果我们能将集合转化到我们熟知的实数系，就能用上更多好用的运算工具（比如微积分）。为了实现这一点，我们需要引入随机变量这一概念：
随机变量的定义
从直观上理解，假设存在 2 个可测空间 $(\Omega,\mathcal{F})$ 和 $(\text{R},\mathcal{B})$ ，那么随机变量 X 就是这样的一个函数关系 $X:\Omega \rightarrow \text{R}$，其作用相当于为 $\mathcal{F}$ 中的每一个元素（即事件）都安排一个对应的实数，从而将 $ ( \Omega, \mathcal{F}, \mathbb{P} )$ 引导到了一个新的概率空间 $ ( \text{R}, \mathcal{B}, \mathbb{L} )$ 上。
随机变量 $X$ 是一个数值的量，其具体数值由 $\omega \in \Omega$ 的随机试验所确定，可以视作样本空间 $\Omega$ 里事件的别名。因此，我们原本对「事件发生可能性大小」的注意力，就可以转移到对「随机变量 $X$ 取不同值的概率」了。不过，在很多时候，$X$ 取特定值的概率都是 0 。因此，我们将主要考虑 $X$ 取值在某一集合上的概率（即 $\mathbb{P}\lbrace X \in 某个集合\rbrace$），而不是取特定值的概率（即 $\mathbb{P}\lbrace X = 某个特定值\rbrace$)。下一节里我们将通过理解随机变量的分布，了解计算 $X$ 取值在某一集合上的概率。
瞅瞅随机变量取值有啥特征——分布测度 $\mu_X$、累积分布函数 $F$ 与……
简单来说，随机变量的分布用于揭示随机变量 2 方面的信息：1. 可以取到哪些值？2. 取得这些值（连续情况下，则是某一区间）的概率分别是多少？。这种分布，可以通过分布测度，或概率质量函数，或密度函数，进行描述。
先来看个例子。回顾我们一开始「连续投掷2次硬币」随机试验结果的空间 $ ( \Omega, \mathcal{F}, \mathbb{P} )$。给定一个随机变量 $S$，用于表示股票价格，其定义如下：
$$ \begin{align} S_0(\omega) &= 4, \forall \omega \in \Omega \\ S_1(\omega) &= \begin{cases} 8, & 如果 \omega_1=H \ 2, & 如果 \omega_1=T \ \end{cases} \\ S_2(\omega) &= \begin{cases} 16, & 如果 \omega_1=\omega_2=H \ 4, & 如果 \omega_1\neq \omega_2 \ 1, & 如果 \omega_1=\omega_2=T \end{cases} \end{align} $$
这些都是随机变量，它们对于每个可能的掷币结果结果序列，都指定了相应的数值。藉此我们可以计算这些随机变量取不同值的概率，确定这些随机变量的分布。例如， $$ \begin{align} \mathbb{P}\lbrace S_2&=16\rbrace=\mathbb{P}(\lbrace HH \rbrace)=p^2 \\ \mathbb{P}\lbrace S_2&=4\rbrace=\mathbb{P}(\lbrace HT \rbrace \cup \lbrace TH \rbrace)=2pq \\ \mathbb{P}\lbrace S_2&=1\rbrace=\mathbb{P}(\lbrace TT \rbrace )=q^2 \end{align} $$
可以将 $S_2$ 的分布设想为，将数量为 1 的质量分配到三块地方：1 块大小为 $p^2$ 的质量位于 16；1 块大小为 $2pq$ 的质量位于4；1 块大小为 $q^2$ 的位于 1。这样，我们就能全面了解 $S_2$ 的所有可能取值。
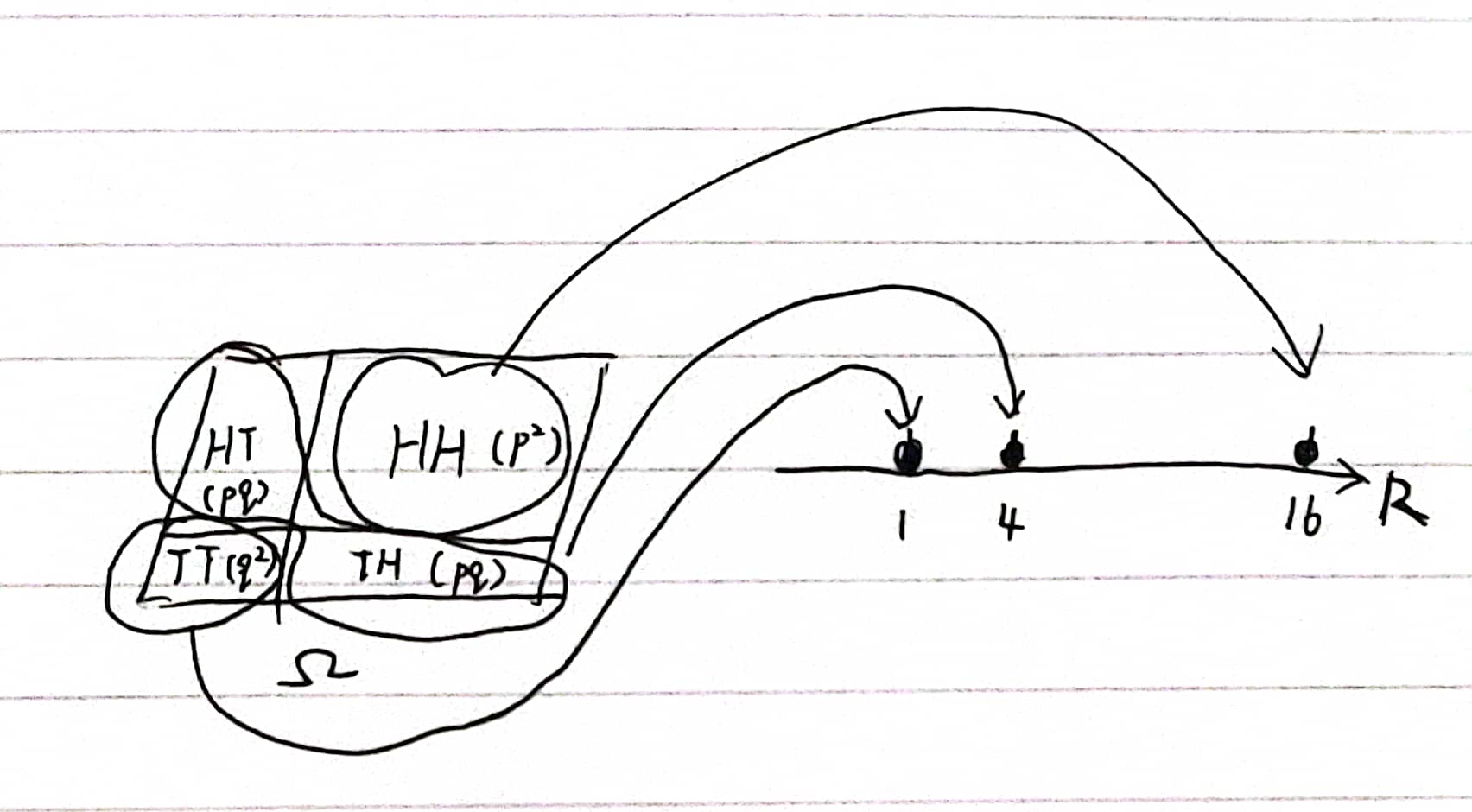
随机变量的用途：将样本空间中的元素映射到实数域中的元素
但是，我们刚才讨论的只是离散情况下的随机变量。如果情况推广到连续情况下，就需要考虑随机变量将单位质量“连续地”分布于整条直线。为此，我们需要将随机变量的分布设想为「在一个集合内有多少质量」，而不是「在某一点有多少质量」。换而言之，随机变量的分布本质上其实也是概率测度，只不过它是在 $\mathbb{R}$ 的子集上的测度。其定义如下：
分布测度的定义
在这个定义中，集合 $B$ 可以仅仅包含一个数。比如说，如果 $B=\lbrace 4\rbrace$，则有 $\mu_{S_2}(B)=2pq$；如果 $B=[2,5]$，我们仍然有 $\mu_{S_2}(B)=2pq$，因为 $S_2$ 在 $[2,5]$ 里只有放在数字 4 的那一块质量。
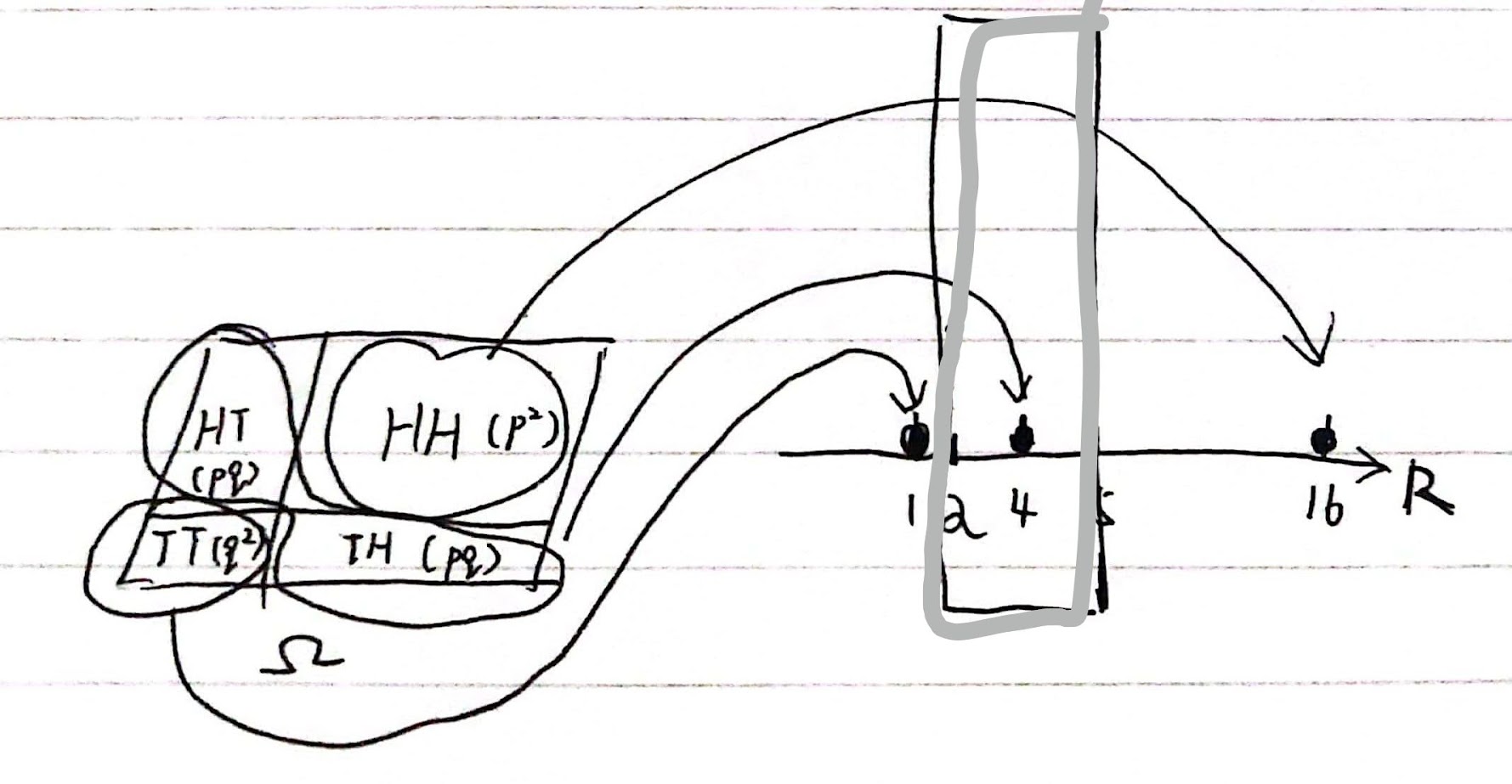
随机变量的用途：将样本空间中的元素映射到实数域中的元素
除了指定分布测度 $\mu_X$ 以外，还有其他记录随机变量的方法。我们可以用累积分布函数来描述随机变量的分布，即：$F(x) = \mathbb{P} \lbrace X\leq x \rbrace, x \in \mathbb{R}$。一方面，如果我们已知分布测度 $\mu_X$ ，则可以通过 $F(x) = \mu_X(-\infty,x]$得到累积分布函数 $F$。另一方面，如果已知累积分布函数 $F$，我们就能计算分布测度 $\mu_X(x,y] = F(y)-F(x)$，其中$x<y $。 在两种特别的情况下，我们可以更详细地描述随机变量的分布。
第一种情况，存在密度函数 $f(x)$，对于所有 $x\in \mathbb{R}$ 有定义，并且满足： $$ \mu_X[a,b] = \mathbb{P}\lbrace a \leq X \leq b\rbrace = \int^b_a f(x)dx, -\infty<a\leq b<\infty $$ 第二种情况，存在概率质量函数，即存在有限序列 $x_1,x_2,\cdots,x_N$ 或者无穷序列 $x_1,x_2,\cdots$ 使得随机变量 $X$ 以概率 1 取序列中的某一个值。定义 $p_i = \mathbb{P}\lbrace X=x_i\rbrace$，则每一个 $p_i$ 非负，并且 $\sum_ip_i=1$。由 $X$ 的分布测度在博雷尔集 $B\subset \mathbb{R}$ 上指定的质量为： $$ \mu_X(B) = \sum_{\lbrace i;x_i \in B\rbrace}{p_i}, B \in \mathcal{B}(\mathbb{R}) $$
某些随机变量的分布可以通过密度函数刻画，而其他的一些随机变量则必须由概率质量函数刻画。不过也存在一些随机变量，其分布由密度函数与概率质量函数混合给出，也有些随机变量的分布既无成块的质量也无密度。
如何知晓随机变量取值的“平均值”——数学期望
设 $X$ 是定义在概率空间 $(\Omega, \mathcal{F}, \mathbb{P})$ 上的随机变量。随机变量的可能取值有很多个，而我们希望计算随机变量的“平均值”，并在计算时考虑到概率的因素。如果 $\Omega$ 是有限空间或者可数的无限空间，便可分别如下计算平均值： $$ \begin{align} \mathbb{E}X &= \sum_{\omega \in \Omega} X(\omega)\mathbb{P}(\omega) \\ \mathbb{E}X &= \sum_{k=1}^\infty X(\omega_k)\mathbb{P}(\omega_k) \end{align} $$ 然而，如果$\Omega$ 是不可数的无限空间，由于不可数的无穷和不能定义，我们只能借助其它工具计算期望。这个工具便是积分。那么，直接用我们之前微积分里学过的黎曼（Riemann）积分可以吗？不太行，因为黎曼积分基本上是设计给连续光滑函数的，只有在充分小的区间上、函数值的改变也非常小的时候才能取到极限。然而，我们现在设计的函数是随机变量，其定义域是事件的集合 $\mathcal{F}$，因此按定义域划分的原则就很难采用：一方面，将 $\mathcal{F}$ 划分为可测集的和，再让这些集合的概率测度趋于 0 ，这种划分方法未必存在；另一方面，即便前面所述的划分方式存在，也只适用于那些在概率测度充分小的集合上 $X$ 的取值改变很小的特殊情况。
因此，我们采用勒贝格积分，通过将函数值域划分为小区间，并进行加总，从而将随机变量的数学期望这个概念转化成了在概率空间 $(\Omega, \mathcal{F}, \mathbb{P})$ 上以概率测度 $\mathbb{P}$) 为积分算子，以随机变量 $X$ 为被积函数的勒贝格积分。
设 $X$ 是概率空间 $(\Omega, \mathcal{F}, \mathbb{P})$ 上的随机变量。勒贝格积分具有下图中的基本性质[^5]：
了解了勒贝格积分的性质后，便可对随机变量的期望进行定义：
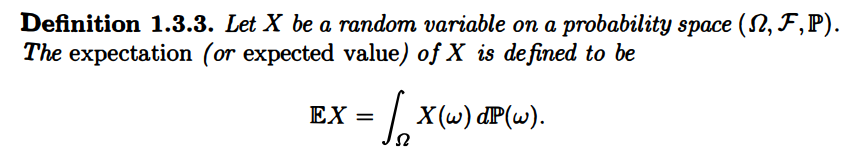根据勒贝格积分的性质，可得期望的性质：
下面的定理给出了黎曼积分与勒贝格积分之间的关系。可以说，只要黎曼积分有定义，黎曼积分和勒贝格积分就一定相等，需要计算时，就可以利用微积分学过的计算黎曼积分的技巧处理勒贝格积分。
拓宽极限的概念——随机变量的收敛方式
本节介绍随机变量序列的几种收敛方式——几乎必然收敛、概率收敛、分布收敛和依 m 阶矩收敛以及它们之间的关系。值得一提的是，随机变量序列的几乎必然收敛、概率收敛分别对应一般测度空间上可测函数序列的几乎处处收敛、测度收敛。
以概率 1 收敛
假设 $\lbrace X_n \rbrace_{n \geq 1}$ 是一组定义在概率空间 $ (\Omega, \mathcal{F}, \mathbb{P})$ 上的随机变量序列，$X$ 是定义在同一空间上的随机变量。如果有 $N \in \mathcal{F}$，且 $\mathbb{P}(N)=0$，则对于所有 $\omega \notin N$，随机变量序列 $\lbrace X_n \rbrace_{n \geq 1}$ 在一般意义上收敛于 $X(\omega)$ ，即： $$ \mathbb{P}\lbrace \omega:\lim_{n \to \infty} X_n(\omega) = X(\omega) \rbrace =1 $$ 则称 $\lbrace X_n \rbrace_{n \geq 1}$ 几乎必然或者以概率 1 收敛于$X$，记作：$X_n \stackrel{a.s.} \longrightarrow X$ 或者 $X_n \longrightarrow X \quad w.p.1$。
以概率收敛
假设 $\lbrace X_n \rbrace_{n \geq 1}$ 是一组定义在概率空间 $ (\Omega, \mathcal{F}, \mathbb{P})$ 上的随机变量序列，$X$ 是定义在同一空间上的随机变量。如果对任何 $\epsilon > 0$ ，有： $$ \lim_{n \to \infty} \mathbb{P}(|X_n-X|>\epsilon) = 0 $$ 则称 $\lbrace X_n \rbrace$ 以概率收敛于$X$，记为 $X_n \stackrel{P} \longrightarrow X$ 。这表明随机变量 $X_n$ 与 $X$ 发生任意确定的正偏差的概率随着n的无限增大而趋近于 0 。
依分布收敛
假设 $\lbrace X_n \rbrace_{n \geq 1}$ 是一组定义在概率空间 $(\Omega, \mathcal{F}, \mathbb{P})$ 上的随机变量序列，设 $\lbrace X_n \rbrace$ 的分布函数是 $\mathcal{D}_n, n=1,2,\cdots$，$X$ 的分布函数是 $\mathcal{D}$。如果对于 $\mathcal{D}$ 的每一个连续点 $x$ 都有：
$$ \lim_{n\to \infty} \mathcal{D}_n(x) = \mathcal{D}(x) $$ 则称 $\lbrace X_n \rbrace$ 依分布收敛于$X$，记为 $X_n \stackrel{\mathcal{D}} \longrightarrow X$ 。
依 m 阶矩收敛
假设 $\lbrace X_n \rbrace_{n \geq 1}$ 是一组定义在概率空间 $ (\Omega, \mathcal{F}, \mathbb{P})$ 上的随机变量序列，$X$ 是定义在同一空间上的随机变量。如果： $$ \lim_{n \to \infty}E(X_n-X)^m=0 $$ 则称 $X_n$ 依 $m$ 阶矩（moment）收敛于 $X$ 。特别地，当 $m=1$ 时称为均值收敛，$m=2$时称为在均方意义上收敛（mean square convergence）。
这几种收敛方式的关系如下图所示[^6]。其中，箭头符号代表起始端点代表的收敛方式蕴含终点端点代表的收敛方式。
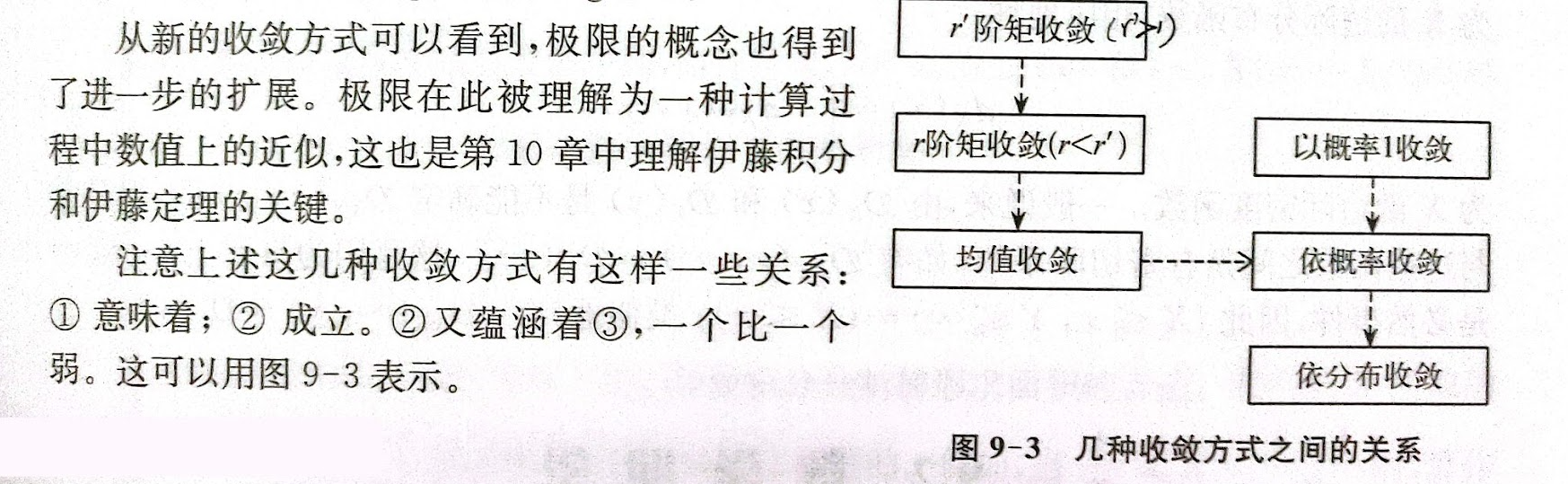
随机变量的收敛方式
总结
本文简单介绍了基于测度论的概率论，以随机试验的样本空间 $\Omega$ 为起点，在此基础上选取了 $\Omega$ 中使概率有定义的子集族 $\mathcal{F}$，并且定义了从 $\mathcal{F}$ 映射到 $[0,1]$ 的函数 $\mathbb{P}$，称之为概率测度。样本空间 $\Omega$ 、子集族 $\mathcal{F}$、概率测度 $\mathbb{P}$ 一同组成了概率空间 $ ( \Omega, \mathcal{F}, \mathbb{P} )$ ，该空间以 $\mathbb{P}(\Omega) = 1$ 及 可数可加性：互不相交集合的概率等于各集合的概率之和 为 2 条公理。
在此基础上，本文介绍了随机变量及其分布。从直观上理解，假设存在 2 个可测空间 $(\Omega,\mathcal{F})$ 和 $(\text{R},\mathcal{B})$ ，那么随机变量 X 就是这样的一个函数关系 $X:\Omega \rightarrow \text{R}$，其作用相当于为 $\mathcal{F}$ 中的每一个元素（即事件）都安排一个对应的实数，从而将 $ ( \Omega, \mathcal{F}, \mathbb{P} )$ 引导到了一个新的概率空间 $ ( \text{R}, \mathcal{B}, \mathbb{L} )$ 上。随机变量 $X$ 是一个数值的量，其具体数值由 $\omega \in \Omega$ 的随机试验所确定，可以视作样本空间 $\Omega$ 里事件的别名。
另外，本文简单介绍了随机变量期望的定义方式：勒贝格积分，以及随机变量的收敛方式：几乎必然收敛、概率收敛、分布收敛和依 m 阶矩收敛。
参考文献
- Stochastic Calculus for Finance II: Continuous-Time Models
- [微观金融学及其数学基础](